
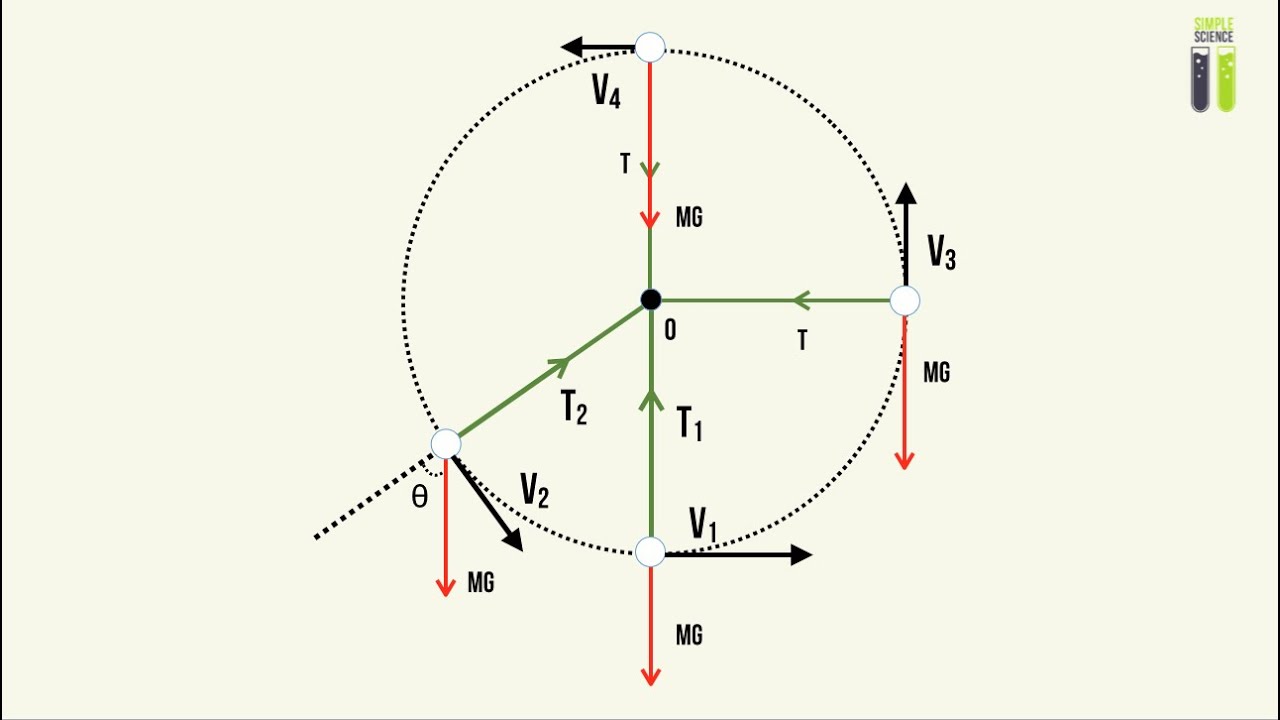
For the same radius of curvature, the acceleration of the object varies _ (directly, inversely) with the speed of the object.Ĭ. For the same speed, the acceleration of the object varies _ (directly, inversely) with the radius of curvature.ī. Thinking Mathematically: Explore the quantitative dependencies of the acceleration upon the speed and the radius of curvature. If the acceleration of the body is towards the center, what is the direction of the unbalanced force? Using a complete sentence, describe the direction of the net force which causes the body to travel in a circle at constant speed.Ĩ. In what direction must a force be applied in order for the object to move back to point D along the path of the circle? Draw an arrow on the diagram. Repeat the above procedure for an object moving from C to D'. In what direction must a force be applied to force the object back towards B? Draw an arrow on the diagram in the direction of the required force.
Suppose that at point A the object traveled in a straight line at constant speed towards B'. A "Thought Experiment": Suppose that an object is moving in a clockwise circle (or at least trying to move in a circle). How can an object accelerate towards the center without ever getting any closer to the center?ħ. It maintains a circular path at a constant radius from the circle's center. A Puzzling Question to Think About: If an object is in uniform circular motion, then it is accelerating towards the center of the circle yet the object never gets any closer to the center of the circle.
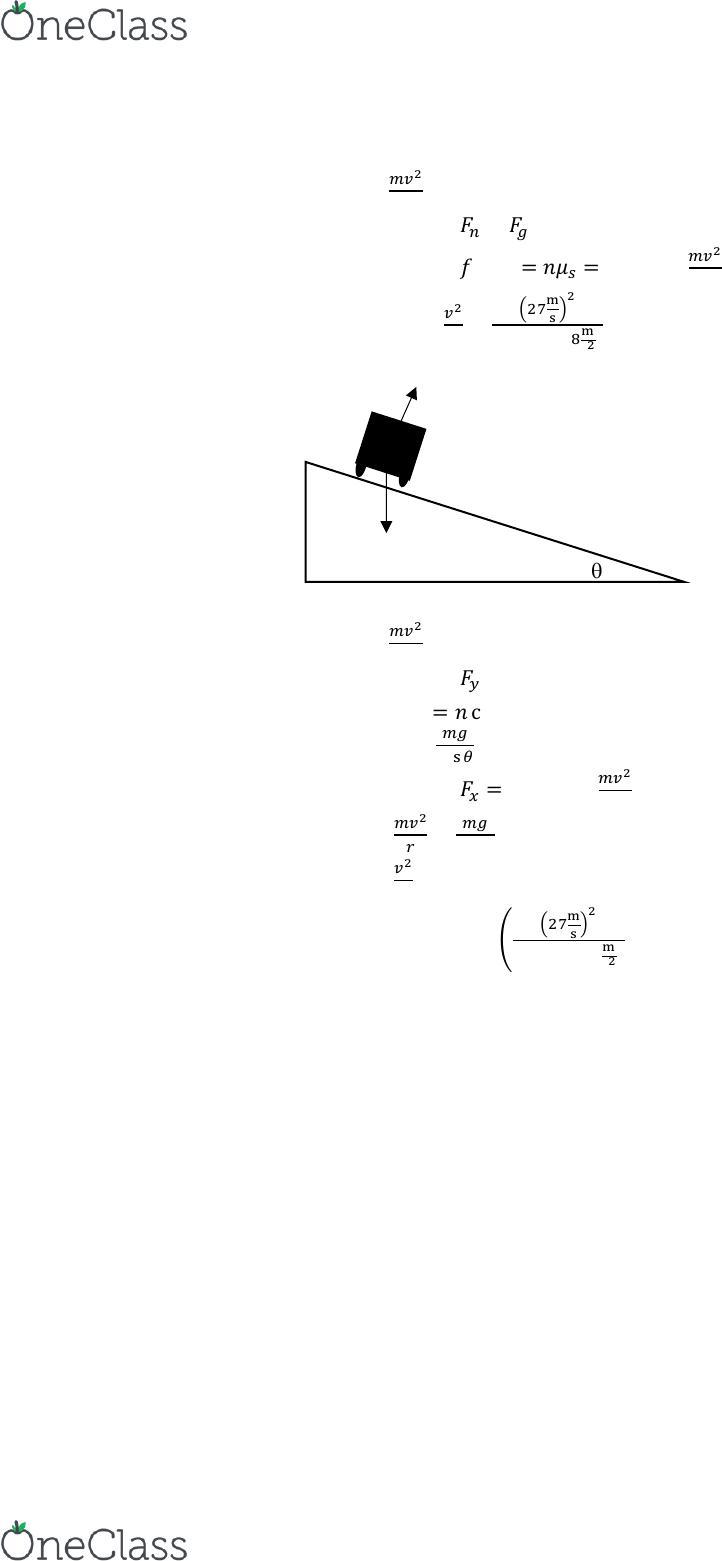
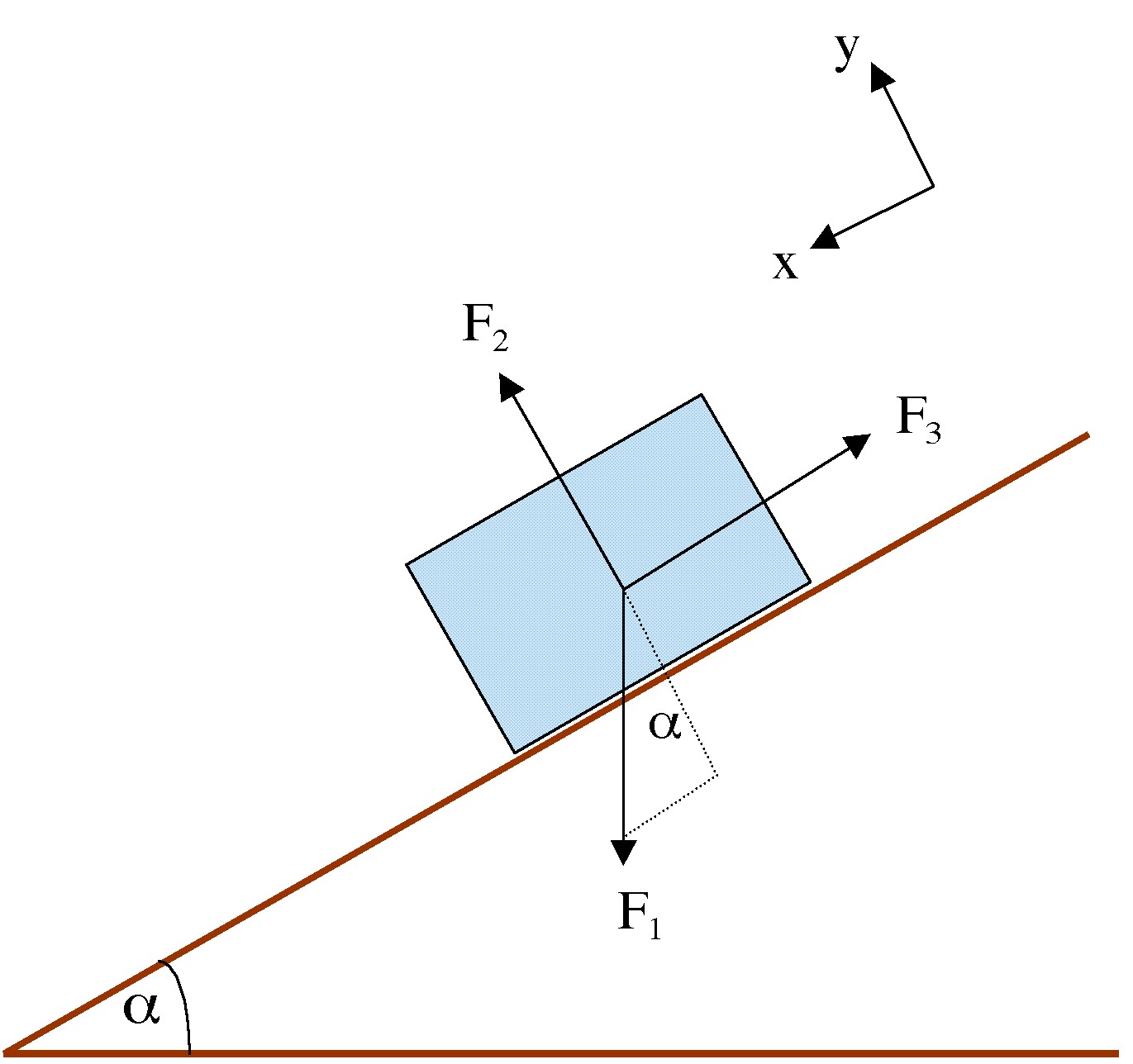
Describe the relationship between the direction of the velocity vector and the direction of the acceleration for a body moving in a circle at constant speed.Ħ. Draw the acceleration vector at the various positions direct the a arrows in the proper direction and label them as a.ĥ. Draw the velocity vector at the various positions direct the v arrows in the proper direction and label them as v. In the diagram at the right, a variety of positions about a circle are shown. If an object moves in a circle at a constant speed, its velocity vector will be constant.Ĥ. Comment on both the magnitude and the direction. Using complete sentences, describe the body's velocity. Velocity is a vector quantity which has both magnitude and direction. The animation can be started, paused, continued or rewound.Īfter gaining familiarity with the program, use it to answer the following questions:Ģ. The acceleration of and the net force acting upon the object are displayed at the bottom of the screen. A trace of the objects motion can be turned on, turned off and erased. The vector nature of velocity and acceleration can be depicted on the screen. The object speed, radius of the circle, and object mass can be varied by using the sliders or the buttons. Navigate to the Uniform Circular Motion page and experiment with the on-screen buttons in order to gain familiarity with the control of the animation. Ω 2 = `(gsinθ)/(rcosθ)` ….The purpose of this activity is to explore the characteristics of the motion of an object in a circle at a constant speed.ġ. The horizontal component T 0 sinθ then becomes the resultant force which is centripetal. The vertical component (T 0 cos θ) balances the weight ‘mg’.As the motion of the bob is a horizontal circular motion, the resultant force must be horizontal and directed towards the centre C of the circular motion.įor this, tension (T 0) in the string is resolved into.the force ‘T 0’ due to the tension in the string, directed along the string, towards the support A. its weight ‘mg’ directed vertically downwardsī. In a given position B, the forces acting on the bob areĪ.Here, θ is the angle made by the string with the vertical, at any position (semi-vertical angle of the cone) Consider the vertical section of a conical pendulum having bob (point mass) of mass m and string of length ‘L’.Such a system is called a conical pendulum. A tiny mass (assumed to be a point object and called a bob) connected to a long, flexible, massless, inextensible string, and suspended to rigid support revolves in such a way that the string moves along the surface of a right circular cone of the vertical axis and the point object performs a uniform horizontal circular motion.


 0 kommentar(er)
0 kommentar(er)
